광도(Lumimosity)의 정의 및 항성의 광도, 유효온도, 반경
광도는 천체가 단위 시간 동안 빛으로 방출되는 총 에너지이다. 광도는 거리와 무관한 천체의 고유 물리량이다. 국제 단위계(SI)에서는 와트(W), CGS 단위계에서는 erg/s를 단위로 사용하지만, 천문학에서는 그 값이 매우 크기 때문에 종종 태양의 광도, 𝐿⊙ (3.828×10^26 W)를 기본 단위로 사용한다.
항성의 광도는 항성 표면에서 잰 총복사속(total radiation flux)과 표면 면적의 곱과 같다. 항성 표면의 총복사속은 유효온도의 4제곱에 비례하며, 표면의 총면적은 반경의 제곱에 비례하므로, 광도는 유효온도의 4제곱과 반경의 제곱에 비례한다. 또 항성의 광도는 지구에서 잰 항성의 총복사속을 의미하는 총조도(total irradiance)와 거리의 제곱에 비례한다. 총조도는 항성의 겉보기 밝기를 의미하며, 그 로그값은 겉보기 등급(apparent magnitude)과 연결된다. 이에 비해 광도는 항성의 절대 밝기를 의미하며, 그 로그값은 절대등급(absolute magnitude, 엄밀히 말하면 절대복사등급)과 연결된다.
항성의 광도, 유효온도, 반경
항성의 광도(L𝐿)는 항성 표면의 총복사속(F𝐹)과 항성의 표면적의 곱과 같다.

항성 표면의 총복사속은 항성 표면에서 단위 시간 동안 단위 면적당 빛으로 방출되는 총 에너지를 의미한다. 항성 표면은 흑체가 아니지만, 항성 표면의 총복사속은 흑체복사에서 성립하는 스테판-볼츠만 법칙을 차용하여 표현한할 수 있다. 이때 스테판-볼츠만 법칙에 사용하는 온도를 유효온도(effective temperature)라 하고, Te𝑇e로 표시한다. 즉

이다. 여기에서 𝜎는 슈테판-볼츠만상수이다. 유효온도는 광도처럼 각 항성의 고유한 물리량이며, 항성의 표면온도로 간주된다. 실제로 빛을 내는 항성 대기에서는 온도가 높이에 따라 변하는 데, 가장 많이 빛을 내는 곳은 온도가 유효온도와 같은 곳이다. 위의 두 식을 결합하면, 광도(𝐿)는 다음과 같이 유효온도(𝑇e)와 반경(𝑅)에 의존한다.

광도가 큰 별은 표면온도가 높거나, 크기가 큰 별임을 알 수 있다.
항성의 광도, 총조도, 광도거리
항성의 총조도(𝑓)는 지구에서 잰 항성의 총복사속이다. 지구에서 단위 시간동안 단위 면적당 입사하는 빛의 총 에너지이다. 광도는 항성의 절대 밝기를 의미하며, 총조도는 항성의 겉보기 밝기를 의미한다. 항성의 광도와 총조도와 거리(𝑑)는 다음과 같이 서로 연결된다.

항성의 겉보기등급은 관측으로 측정할 수 있고, 이로부터 𝑓를 이끌어낼 수 있다. 별도의 방법으로 𝐿을 결정할 수 있다면, 𝑓와 𝐿로부터 거리 𝑑을 구할 수 있다. 이렇게 정의된 거리를 광도거리(luminosity distance)라고 한다. 광도거리 𝐷𝐿은
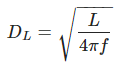
으로 정의된다.
H-R도와 광도등급
H-R도는 별의 표면온도와 광도 사이의 상관관계를 보여준다(그림 참조). 1920년대에 헤르츠스프룽(Ejnar Hertzsprung)과 러셀(Henry Norris Russell)이 독립적으로 사용하였다. H-R도는 천문학에서 가장 중요한 그림 중 하나로서 별의 물리적인 특성과 별의 진화를 연구하는 데에 매우 유용하게 사용된다.
H-R도를 보면 별들이 대표적인 4개의 무리인 주계열(main sequence), 초거성(supergiants), 거성(giants), 그리고 백생외성(white dwarfs)로 구분될 수 있음을 알 수 있다. 분광형이 같더라도 별의 반지름에 따라 광도가 상당히 달라짐을 알 수 있는데 이를 종종 광도계급(luminoisty class)이라고 부른다. 광도 계급에는 초거성(Ia,Ib), 밝은 거성(Ⅱ), 거성(Ⅲ), 준거성(Ⅳ), 주계열성(Ⅴ)이 있다.

질량-광도의 관계
주계열에 속하는 항성들은 질량과 광도가 아래와 같이 밀접한 연관이 있음이 알려져 있다.

여기에서 𝐿⊙ 과 𝑀⊙은 각각 태양의 광도와 질량이고 1<𝑎<6이다. 별의 질량에 따라 𝑎 값이 달라지는데 별의 질량에 따른 관계식을 요약하면 다음과 같다.
